جدول المحتويات:
سمات القيمة المطلقة
تتصف القيمة المطلقة بعدة خصائص هامة ومميزة، وهي تساعد في تبسيط العمليات الحسابية وحل المعادلات. من بين هذه الخصائص:
- |أ| ≥ 0: هذه الخاصية تعني أن نتيجة القيمة المطلقة لأي عدد حقيقي (أ) ستكون دائماً أكبر من أو تساوي الصفر.
- |أ| = √(أ²): القيمة المطلقة للعدد (أ) تساوي الجذر التربيعي لمربع هذا العدد. هذه الخاصية تؤكد أن النتيجة ستكون دائماً موجبة أو صفر.
- |أ × ب| = |أ| × |ب|: القيمة المطلقة لحاصل ضرب عددين (أ) و (ب) تساوي حاصل ضرب القيمة المطلقة لكل من العددين.
- |أ| = |-أ|: العدد ونظيره الجمعي لهما نفس القيمة المطلقة.
- |أ – ب| = |ب – أ|: القيمة المطلقة للفرق بين عددين (أ) و (ب) متساوية بغض النظر عن ترتيب العددين.
- |أ| = |ب| إذا وفقط إذا كانت أ = ب أو أ = -ب
- |أⁿ| = |أ|ⁿ، حيث ن عدد صحيح موجب.
- |أ / ب| = |أ| / |ب|، حيث ب لا تساوي صفر.
- |أ ± ب| ≤ |أ| + |ب|: هذه الخاصية المعروفة باسم متباينة المثلث، تشير إلى أن القيمة المطلقة لمجموع أو فرق عددين أقل من أو تساوي مجموع القيم المطلقة للعددين.
ملاحظة: المتغيران (أ) و (ب) في الخصائص أعلاه يمثلان أي عددين حقيقيين.
شرح القيمة المطلقة
القيمة المطلقة هي قياس لبعد العدد الحقيقي عن الصفر على خط الأعداد، بغض النظر عن اتجاهه. وبعبارة أخرى، هي قيمة العدد بدون النظر إلى إشارته. فمثلاً، القيمة المطلقة للعدد 5 هي 5، والقيمة المطلقة للعدد -5 هي أيضاً 5. تستخدم القيمة المطلقة بشكل خاص في الحالات التي نهتم فيها بالمقدار فقط، مثل حساب المسافات.
إن القيمة المطلقة تعبر عن المسافة بين العدد والصفر، وهي دائماً قيمة غير سالبة. هذا المفهوم أساسي في العديد من فروع الرياضيات والتطبيقات العملية.
كيفية التعبير عن القيمة المطلقة
للتعبير عن القيمة المطلقة لعدد ما، وليكن (س)، نستخدم الرمز |س|. على سبيل المثال:
- |7| = 7
- |-7| = 7
هذا الرمز يعني ببساطة أننا نهتم بالقيمة العددية فقط، ونتجاهل الإشارة. وبالتالي، فإن النتيجة ستكون دائماً موجبة أو صفر.
دالة القيمة المطلقة
دالة القيمة المطلقة هي دالة رياضية تحول أي عدد حقيقي إلى قيمته الموجبة أو الصفر. يمكن التعبير عنها بالصيغة التالية:
ق(س) = |س|
خصائص هذه الدالة:
- مجالها: جميع الأعداد الحقيقية.
- مداها: جميع الأعداد الحقيقية غير السالبة (أكبر من أو تساوي الصفر).
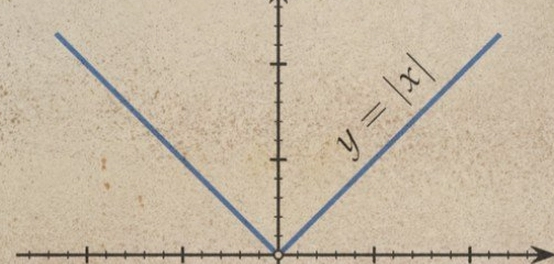
- التمثيل البياني: يشبه حرف (V)، ويقع بالكامل فوق محور السينات.
- التماثل: متماثلة حول محور الصادات.
تطبيقات وأمثلة متنوعة للقيمة المطلقة
أمثلة توضيحية
فيما يلي بعض الأمثلة المتنوعة التي توضح كيفية استخدام القيمة المطلقة في حل المسائل الرياضية:
المثال الأول: احسب قيمة ما يلي:
| السؤال | الحل |
|---|---|
| |3.5| – |-2.5| | |3.5| – |-2.5| = 3.5 – 2.5 = 1 |
| |5 × 6| | |5 × 6| = |30| = 30 |
| |2 × (2/3 – 0.5)| | |2 × (2/3 – 0.5)| = |2 × (1/6)| = |1/3| = 1/3 |
| ||-12| – √(|-4|)²| | ||-12| – √(|-4|)²| = |12 – √(16)| = |12 – 4| = 8 |
| |³√(-3)+5| | |³√(-27)+5| = |-3+5| =|2| = 2 |
المثال الثاني: حل المعادلة |س + 2| = 5
الحل:
س + 2 = ±5
إذاً، س + 2 = 5 أو س + 2 = -5
الحلول هي: س = 3 أو س = -7
المثال الثالث: أوجد مدى قيم س في المتباينة |س| < 3.
الحل:
يمكن كتابة هذه المتباينة على شكل -3 < س < 3.
المثال الرابع: أوجد مدى قيم س في المتباينة |3س – 6| ≤ 12.
الحل:
-12 ≤ 3س – 6 ≤ 12
-6 ≤ 3س ≤ 18
-2 ≤ س ≤ 6
المثال الخامس: حل المعادلة |س – 2| + |س – 3| = 1
الحل:
بتحليل الحالات المختلفة لعلامات (س-2) و (س-3)، نجد أن الحلول هي: 2 ≤ س ≤ 3
المثال السادس: حل المعادلة |3س – 2| = |5س + 4|.
الحل:
3س – 2 = 5س + 4 أو 3س – 2 = -(5س + 4)
الحلول هي: س = -3 أو س = -1/4
المثال السابع: إذا كانت س = 2، فما قيمة |-4س + 3| × |3س – 14|؟
الحل:
|-4(2) + 3| × |3(2) – 14| = |-8 + 3| × |6 – 14| = |-5| × |-8| = 5 × 8 = 40
المثال الثامن: إذا كان |2أ – 3| = 5 و |3 – 4ب| = 11، وأ و ب عددان سالبان، فما قيمة |ب – أ|؟
الحل:
من |2أ – 3| = 5، نجد أن أ = -1 (لأنها سالبة)
من |3 – 4ب| = 11، نجد أن ب = -2 (لأنها سالبة)
إذاً، |ب – أ| = |-2 – (-1)| = |-1| = 1
القيمة المطلقة أداة قوية في الرياضيات، ولها تطبيقات واسعة في مختلف المجالات. فهم خصائصها واستخداماتها يمكن أن يسهل حل العديد من المسائل المعقدة.