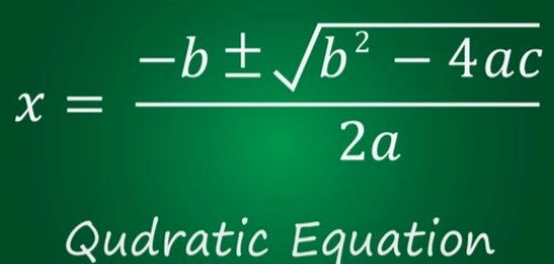طرق تفكيك المعادلة التربيعية
المعادلة التربيعية، أو معادلة الدرجة الثانية، هي معادلة يمكن كتابتها على الصورة التالية:
أ س² + ب س + ج = 0
حيث أن: أ، ب، ج هي ثوابت عددية، يمكن أن تكون موجبة أو سالبة، مع ملاحظة أن الثابتين (ب، ج) يمكن أن يساويا الصفر. يُطلق على ‘أ’ معامل س²، وعلى ‘ب’ معامل س، وعلى ‘ج’ الحد الثابت. أعلى قوة للمتغير ‘س’ في المعادلة التربيعية هي 2. أمثلة على عبارات تربيعية:
- س²-7س+11
- 4س²+3س-1
- س²+8س
- 3س²+2
عملية تحليل المعادلة التربيعية تعني إعادة كتابتها كحاصل ضرب عاملين أو أكثر في أبسط صورة ممكنة. على سبيل المثال:
- المعادلة 2س²+10س يمكن تحليلها إلى: 2س(س+5).
- المعادلة س²-16 يمكن تحليلها إلى: (س-4)(س+4).
الاعتماد على التقدير في التحليل
تستخدم هذه الطريقة لتحليل المعادلات التربيعية المكتوبة بالصورة القياسية: أس²+ب س+ج=0. الفكرة الأساسية هي إيجاد عددين يكون مجموعهما يساوي ‘ب’، وحاصل ضربهما يساوي ‘أ’ مضروبة في ‘ج’. قد تكون بعض المعادلات التربيعية معقدة، مما يستدعي استخدام طرق أخرى مثل القانون العام أو إكمال المربع.
عندما يكون معامل س² يساوي 1
لتحليل المعادلة عندما أ=1:
- أوجد عددين حاصل جمعهما يساوي ‘ب’، وحاصل ضربهما يساوي ‘ج’.
- اكتب المعادلة التربيعية على الصورة: (س+ك)(س+ل)، حيث ‘ك’ و ‘ل’ هما العددان اللذان تم إيجادهما. مثال: إذا كان العددان هما 1 و -2، تُكتب المعادلة كالتالي: (س+1)(س-2).
مثال: لتحليل المعادلة س²+س-6=0، نبحث عن عددين مجموعهما 1 وحاصل ضربهما -6. العددان هما -2 و 3. إذن، س²+س-6=(س-2)(س+3)=0.
عندما يكون معامل س² لا يساوي 1
لتحليل المعادلة عندما أ≠1:
- أوجد حاصل ضرب أ×ج.
- أوجد عددين حاصل جمعهما يساوي ‘ب’، وحاصل ضربهما يساوي أ×ج. لنفترض أنهما العددان ‘ك’ و ‘ل’.
- استبدل الحد (ب س) بـ (ك+ل)س، لتصبح المعادلة: أس²+(ك+ل)س+ج=0، ثم: أس²+ك س+ل س+ج=0.
- حلل أول حدين (أس²+ك س) بأخذ العامل المشترك، ثم حلل آخر حدين (ل س+ج) بنفس الطريقة.
- أخرج عامل مشترك لكتابة المعادلة التربيعية كحاصل ضرب حدين.
مثال: لتحليل المعادلة 4س²+15س+9=0، أولاً نجد 4×9=36. ثم نبحث عن عددين مجموعهما 15 وحاصل ضربهما 36، وهما 3 و 12. نكتب المعادلة كالتالي: 4س²+3س+12س+9=0. نحلل أول حدين (س كعامل مشترك) وآخر حدين (3 كعامل مشترك): س(4س+3)+3(4س+3)=0. ثم نأخذ (4س+3) كعامل مشترك: (4س+3)(س+3)=0.
التعامل مع الفرق بين مربعين
يمثل الفرق بين مربعين طرح مربع عدد أو متغير من مربع عدد أو متغير آخر. هذه حالة خاصة من المعادلات التربيعية، وصورتها العامة هي: أ²-ب²؛ مثل: س²-36. للتحليل، يمكن كتابتها كالتالي:
أ²-ب²=(أ + ب) ( أ – ب)
حيث أن:
- أ: الجذر التربيعي للحد الأول.
- ب: الجذر التربيعي للحد الثاني.
مثال: لتحليل س²-16، نأخذ الجذر التربيعي للحدين: س²-16=(س-4)(س+4). وبالمثل، 4س²-36=(2س-6)(2س+6)=0.
تطبيق القانون العام
يستخدم القانون العام عندما تفشل الطرق الأخرى في تحليل المعادلة التربيعية. القانون العام هو:
س= (- ب ± √(ب²- 4 أ ج)) / 2 أ
هذه الصيغة تعطي حلين: س+ و س-. تُستخدم لكتابة المعادلة على الصورة: أ(س-س-)(س-س+).
مثال: لتحليل 6س²+5س-6، نعوض أ=6، ب=5، ج=-6 في القانون العام: س= (-5 ± √(5²-4×6×-6))/(2×6)، ومنه: س=-5±√(169)/12، فبالتالي: س=-5±13/12، إذن: س-=(-5-13)/12=-3/2، س+=(13-5)/12=2/3. ثم نعوض القيمتين في المعادلة: 6 س²+5 س-6=6(س+3/2)(س-2/3)=(3س+2)(2س-3)
ملاحظة مهمة: في القانون العام، الجزء (ب²- 4 أ ج) الموجود تحت الجذر التربيعي يسمى المميز. إذا كان المميز سالباً، فإنه لا يوجد حل حقيقي للمعادلة التربيعية، بل يوجد حلول مركبة (تخيلية).
إكمال المربع كحل بديل
يمكن استخدام طريقة إكمال المربع عندما لا تكون المعادلة مربعًا كاملاً ولا يمكن حلها بالطرق السابقة.
- أضف واطرح (ب/2)² من المعادلة أس² + ب س +ج=0. مثال: في المعادلة س² + 6 س + 7=0، (ب/2)² =(6/2)² =9.
- يصبح شكل المعادلة: أس² + ب س+ (ب/2)² – (ب/2)² +ج=0، أي س² + 6 س+ 9 -9+7=0.
- أعد ترتيب المعادلة: (س+(ب /2))²-((ب/2)²-ج) =0، أي (س+3)²-2=0، وتساوي (س+3)² =2.
- خذ الجذر التربيعي للطرفين: س+3 = ±√(2).
- أوجد قيمة س: س= √(2) -3 أو س= -√(2) -3.
مثال: حل المعادلة س² +2 س -3=0 بإكمال المربع:
- (ب/2)²= (2/2)² = 1. أضف واطرح 1 للمعادلة.
- تصبح المعادلة: س² + 2 س+ 1 -1-3=0.
- أعد كتابة المعادلة: س² + 2 س+1=4.
- الشكل النهائي: (س+1)² =4.
- خذ الجذر التربيعي للطرفين: س+1 = ±2.
- الحل: س=1 أو س=-3.
حالات خاصة للمعادلة التربيعية
تتغير صورة المعادلة التربيعية إذا كان أحد المعاملات يساوي صفرًا. إذا كانت قيمة ‘أ’ تساوي صفرًا، تصبح المعادلة خطية. إذا كانت قيمة ‘ب’ تساوي صفرًا، يكون للمعادلة حلان متساويان بالقيمة ومختلفان بالإشارة. إذا كانت قيمة ‘ج’ تساوي صفرًا، يتم الحل بإخراج عامل مشترك.
أ يساوي صفر
إذا كانت أ=0، تصبح المعادلة خطية على الصورة: ب س + ج = 0.
- انقل الثابت ‘ج’ إلى الطرف الآخر.
- اقسم الطرفين على معامل ‘س’ وهو ‘ب’ لإيجاد قيمة ‘س’.
مثال: حل المعادلة 5 س+20= 0:
- انقل 20 للطرف الثاني: 5 س= -20.
- اقسم على 5: س =-20/5.
- إذاً س=-4.
ب يساوي صفر
إذا كانت ب=0، يصبح شكل المعادلة: أس²+ ج=0، ويكون للمعادلة حلان متساويان في القيمة ومختلفان في الإشارة.
- انقل ‘ج’ للطرف الآخر.
- اقسم الطرفين على معامل س²، وهو ‘أ’.
- خذ الجذر التربيعي للطرفين.
مثال: حل المعادلة 2 س² -30= 0:
- انقل 30 للطرف الثاني: 2س²= 30.
- اقسم الطرفين على 2: س²= 15.
- خذ الجذر التربيعي للطرفين: س= ±√(15).
ج يساوي صفر
إذا كانت ج=0، يصبح شكل المعادلة: أس² + ب س=0.
- أخرج ‘س’ عامل مشترك: س(أس+ب) =0.
- إذن س=0 أو أس+ب=0، أي س = – ب/أ.
مثال: حل المعادلة س² – 81 س=0:
- أخرج ‘س’ عامل مشترك: س(س-81) =0.
- إذن س=0 أو س-81 =0.
- إذاً س=0 أو س=81.
أمثلة تطبيقية على تحليل المعادلة التربيعية
حل المعادلة التربيعية باستخدام طريقة التخمين
مثال (1): حل المُعادلة التربيعيّة الآتية: س²+4 س+3=0
- إيجاد عددين حاصل جمعهما يساوي 4، وناتج ضربهما يساوي 3، وهما 1، و3.
- تُكتب المُعادلة التربيعيّة على صورة: (س+1)(س+3)=0.
- إذاً س= -1، أو س= -3.
مثال (2): حل المُعادلة التربيعيّة الآتية: 6 س²+ 1 س+ -2= 0
- إيجاد حاصل ضرب -2×6=-12.
- إيجاد عددين حاصل جمعهما يساوي 1، وناتج ضربهما -12، وهما 4، -3
- تعويض العددين مكان 1 المُعادلة لينتج 6 س²+(4+-3) س+-2 =0، ومنه: 6 س²+4 س-3 س-2=0.
- تحليل أول حدّين بأخذ 2 س كعامل مُشترك: 2س(3س+2)-(3س+2)=0.
- نخرج (3س+2) عامل مشترك، فتصبح (3س+2)(2 س-1)=0.
- ومنه إما س= 1/2، أو س= -2/3.
حل المعادلة التربيعية باستخدام طريقةالفرق بين مربعين
حل المُعادلة التربيعيّة الآتية: (س² -81)=0
- نحلل المعادلة، ونكتبها على شكل ( س-9)*(س+9) بحيث أن ضرب -9، 9 يساوي 81 وجمع 9،-9 يساوي صفر.
- ومنه إما س =9، أو س= -9.
حل المعادلة التربيعية باستخدام الصيغة العامة
حل المعادلة الآتية باستخدام الصيغة العامة،2س²+9 س+-18= 0
- قيمة أ =2، ب=9، ج=-18.
- نطبق حسب القانون العام : س= (-ب ± √(ب²-4أج))/2أ .
- س = (-9±√(²9 -4*2*-18)) /2*2.
- س= (-9 ±√(225))/4.
- س= (-9±15)/4.
- ومنه إما س=-6، أو س= 3/2.
حل المعادلة التربيعية باستخدام إكمال المربع
حل المعادلة الآتية باستخدام إكمال المربع،س²+ 6 س -2=0
- نجد ب/2، وتساوي 2/6= 3.
- ننقل ج إلى الطرف الآخر عن طريق إضافة +2 للطرفين، تصبح المعادلةس²+ 6 س= 2.
- نجد قيمة (ب/2)² وهي (6/2)² = ²3 =9.
- بعد إضافة وطرح 9 إلى الطرفين تصبح المعادلة كما يأتي: س²+ 6 س+9 = 11.
- نحلل المعادلة إلى (س+3) (س+3) =11 وتكتب (س+3)² = 11.
- نأخذ الجذر للطرفين، فتصبح س= √(11)-3، أو س =-(√(11))-3.
حل المعادلة التربيعية عندما بيساوي صفر
حل المعادلة التربيعية 6 س²+ ب س-42=0، إذا كان قيمة ب =0
- تعويض قيمة ب في المعادلة تصبح كالآتي: 6 س²+ -42=0.
- ننقل 42 للطرف الثاني عن طريق جمع 42 للطرفين، لتصبح المعادلة 6 س²= 42.
- نقسم الطرفين على 6 ، تصبح المعادلة س²= 42/6 .
- نأخذ الجذر للطرفين.
- إذًا قيمة س، هي: س= √(7)+، أو س= √(7)-.
حل المعادلة التربيعية عندما جيساوي صفر
حل المعادلة 2ص²+ 6 ص=0
- نخرج ص عامل مشترك لتصبح ص(2ص+6) =0.
- و منها، ص=0 أو (2ص+6)=0.
- ننقل 6 للطرف الثاني عن طريق طرح 6 من الطرفين لتصبح 2ص= -6.
- نقسم 2 على الطرفين لتصبح القيمة الأخرى ل ص= -3.
- إذًا ص= -3، أو ص=0 .
المصادر
- Factorising quadratics
- Solving a Quadratic Equation: Factorisation
- Factoring Quadratics
- Solving Quadratic Equations by Factoring
- Difference Of Squares
- factoring-quadratics
- How (and When) to Complete the Square: 5 Simple Steps
- How do you solve x 2 + 5 x = 0 ?
- 4.2 Solving linear equations
- Differences Between Quadratic & Linear Equations